【CSS】表（table）の行の背景色を規則的につける方法（コピペOK）

はじめに

記事中に表を作るとき、行ごとに背景色をつけたい場合がありますよね。

例えば、次の画像のように、偶数行をオレンジ色にしたり……

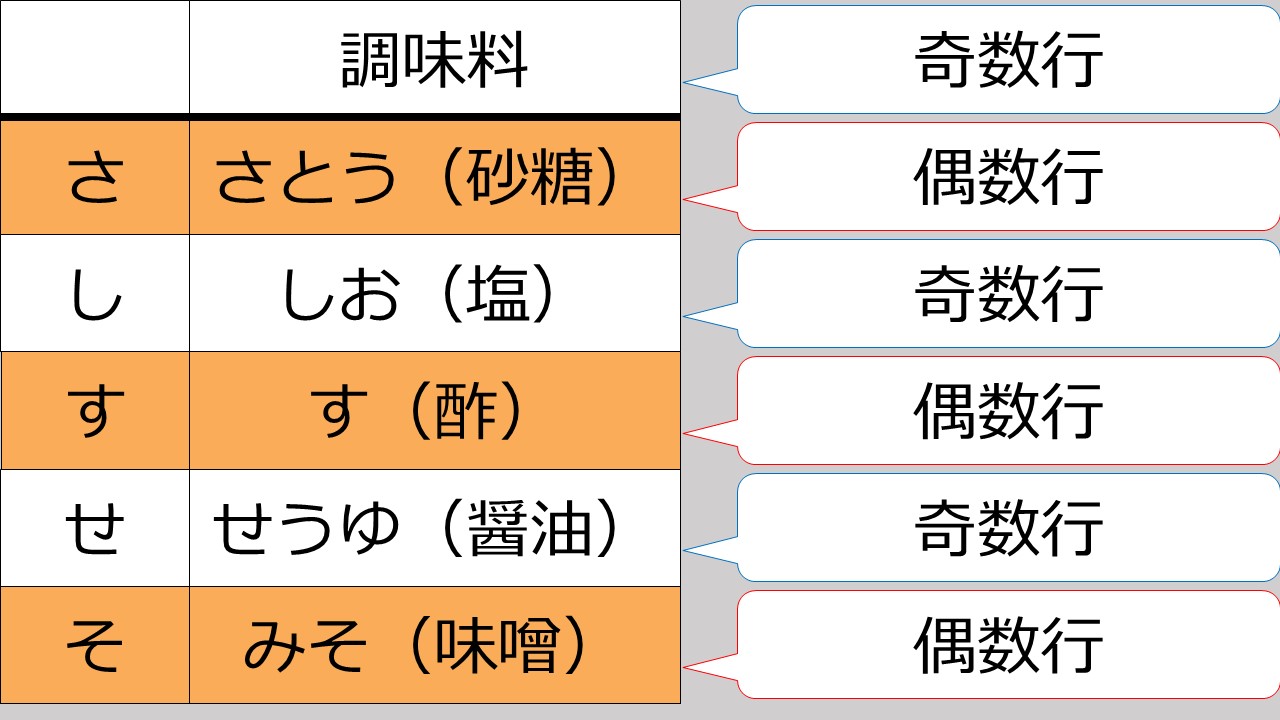
次の画像のように、奇数行を水色にしたり……

次の画像のように、偶数行をオレンジ色にして奇数行を水色にしたり……ですよね。

そこで、この記事では、CSSを使ってtableの行の背景色を規則的につける方法を説明します。

前半部分はコード（例）を掲載し、後半部分はコード中の規則性の考え方を説明します。コードはもちろんコピペOKです。あなたの記事の表のデザインに役立ててください。

tableの行の背景色を規則的につけるCSSの例

表の標準の背景色は「白色（#ffffff）」として説明します。

偶数行に色をつけるCSS

/*2n-1は1行め、3行め、5行め……。*/
table tr:nth-child(2n-1) td
{
  background-color:#ffffff;
}

/*2nは2行め、4行め、6行め……。*/
table tr:nth-child(2n) td
{
  background-color:#faac58;
}

#ffffffは白色で、#faac58はオレンジ色なので、表の背景色は次のようになります。

偶数行（2n）がオレンジ色になっていることがわかります！

コピペのあとは、カラーコード（#～）の部分を好きなように変更してください。

奇数行の色をつけるCSS

/*2n-1は1行め、3行め、5行め……。*/
table tr:nth-child(2n-1) td
{
  background-color:#58acfa;
}

/*2nは2行め、4行め、6行め……。*/
table tr:nth-child(2n) td
{
  background-color:#ffffff;
}

#58acfaは水色で、#ffffffは白色なので、表の背景色は次のようになります。

奇数行（2n-1）が水色になっていることがわかります！

コピペのあとは、カラーコード（#～）の部分を好きなように変更してください。

偶数行にも奇数行にも色をつけるCSS

/*2n-1は1行め、3行め、5行め……。*/
table tr:nth-child(2n-1) td
{
  background-color:#58acfa;
}

/*2nは2行め、4行め、6行め……。*/
table tr:nth-child(2n) td
{
  background-color:#faac58;
}

#58acfaは水色で、#faac58はオレンジ色なので、表の背景色は次のようになります。

奇数行が水色に、偶数行がオレンジ色になっていることがわかります！

コピペのあとは、カラーコード（#～）の部分を好きなように変更してください。

3行のローテーションで色をつけるCSS

/*3n-2は1行め、4行め、7行め……。*/
table tr:nth-child(3n-2) td
{
  background-color:#58acfa;
}

/*3n-1は2行め、5行め、8行め……。*/
table tr:nth-child(3n-1) td
{
  background-color:#faac58;
}

/*3nは3行め、6行め、9行め……。*/
table tr:nth-child(3n) td
{
  background-color:#58fa58;
}

#58acfaは水色で、#faac58はオレンジ色で、#58fa58は黄緑色なので、表の背景色は次のようになります。

水色 → オレンジ色 → 黄緑色 の繰り返しになっていることがわかります！

コピペのあとは、カラーコード（#～）の部分を好きなように変更してください。

tableの行に関する規則性の考え方

すべてに共通して言えることですが、nというのは1以上の整数全部だと考えてください。つまり、1、2、3、4、5……ということですね。

2行のローテーションを表す式

上の画像のような、2行のローテーションを表す式を考えましょう。

まず、偶数行をnで表す方法を考えます。nは1、2、3……ですね。

偶数行は2の倍数行です。2の倍数は、2×1、2×2、2×3……なので、「2×n」でOKだとわかります。

しかし、掛け算の記号は省略しなければならないので、2nが正解です。

次に、奇数行をnで表す方法を考えます。nは1、2、3……ですね。

奇数は、1、3、5……ですが、これをどうやってnで表せば良いのでしょうか。それは、次のとおりです。

• 1 = 2 – 1 = 2×1 – 1
• 3 = 4 – 1 = 2×2 – 1
• 5 = 6 – 1 = 2×3 – 1

つまり、2×n – 1の掛け算記号を省略した、2n – 1が正解です。

したがって、答えは次の画像のとおりです。かっこの中は、「～の場合」という意味です。

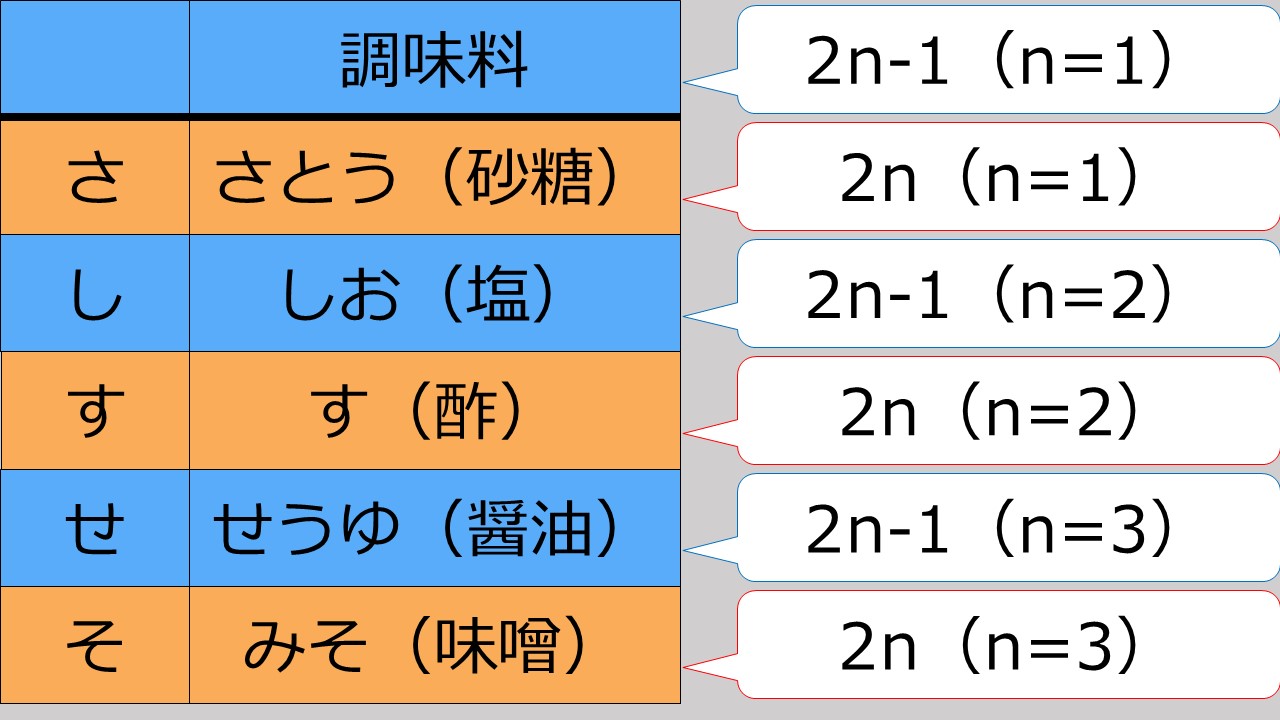
3行のローテーションを表す式

上の画像のような、3行のローテーションを表す式を考えましょう。

まず、3行め、6行め、9行め……の表し方から考えます。nは1、2、3……ですね。

答えを書くと、

• 3 = 3×1 = 3n
• 6 = 3×2 = 3n
• 9 = 3×3 = 3n

と表すことができます。

よって、3nが正解です。

次に、2行め、5行め、8行め……の表し方を考えます。nは1、2、3……ですね。

答えを書くと、

• 2 = 3 – 1 = 3×1 – 1 = 3n – 1
• 5 = 6 – 1 = 3×2 – 1 = 3n – 1
• 8 = 9 – 1 = 3×3 – 1 = 3n – 1

と表すことができます。

よって、3n – 1が正解です。

最後に、1行め、4行め、7行め……の表し方を考えます。nは1、2、3……ですね。

答えを書くと、

• 1 = 3 – 2 = 3×1 – 2 = 3n – 2
• 4 = 6 – 2 = 3×2 – 2 = 3n – 2
• 7 = 9 – 2 = 3×3 – 2 = 3n – 2

と表すことができます。

よって、3n – 2が正解です。

したがって、答えは次の画像のとおりです。かっこの中は、「～の場合」という意味です。

3行のローテーションが式で表現できたら、4行のローテーションも5行のローテーションも表現できるはずです。ぜひ挑戦してみてください。