はじめに
.png)
どうも! みなため(@MinatameT)です。
この記事では、「数学が苦手でわけがわからない!」という人や、数学的センスのない人に向けて、2次方程式の解き方を説明しています。
私は数学の苦手な人の気持ちがわかるので、どのサイトよりもていねいに説明できている自信があります。
かなり初歩的な説明もしつこくしてありますが、ご了承ください。また、最後には確認問題集も用意してあります。

それでは、さっそく説明していきます。少し長くなりますが、頑張りましょう!
解の公式とは?
解の公式とは、2次方程式(xの2乗のついている式)を機械的に解くためのものです。ここでいう「解く」とは、xの値を求めることです。
解の公式を使った解き方は、数学的センスがほぼいらないので、数学が苦手な人(平方完成や因数分解がわからない人)に超おすすめの解き方なのです。
しかし、解の公式はどんな2次方程式にも使えるわけではなく、次のような形式の(右辺を0にした)2次方程式にしか使えません。
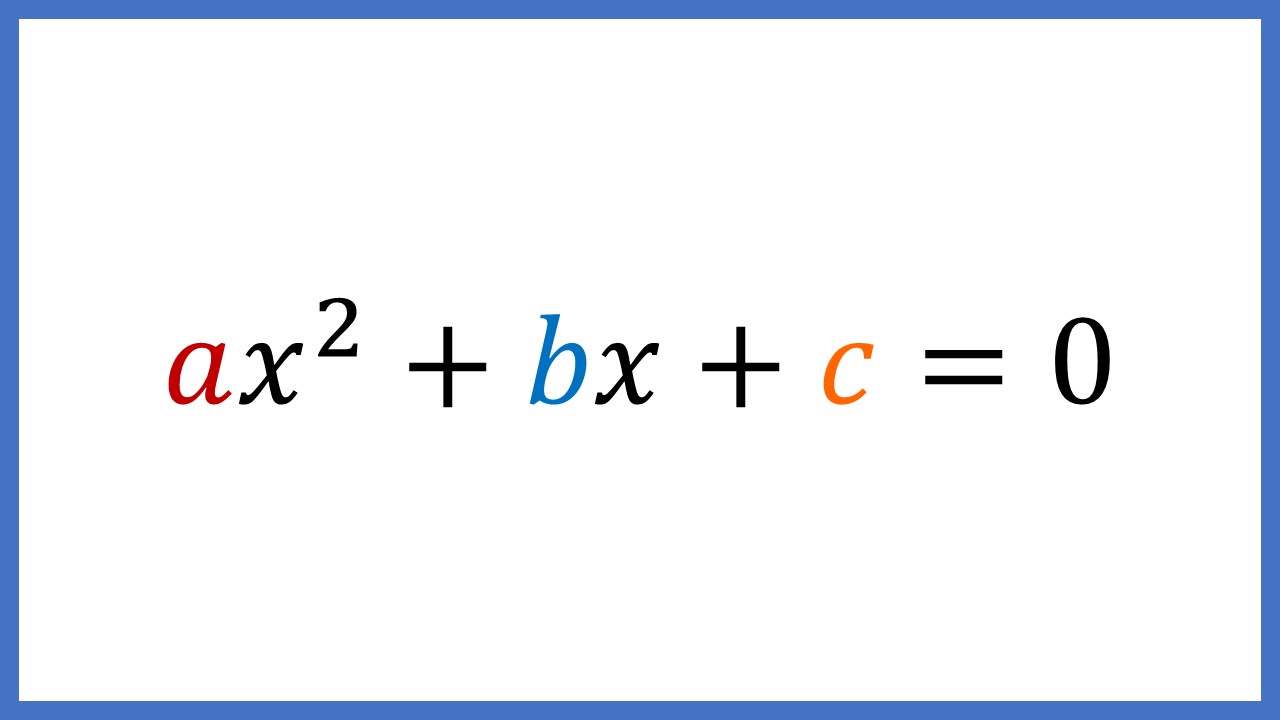
このa、b、cは係数といい、何かの数字が入ります。0が入ってもOKです。下の画像のように、aが0の場合はxの2乗が消えて0になり、bが0の場合はxが消えて0になります。
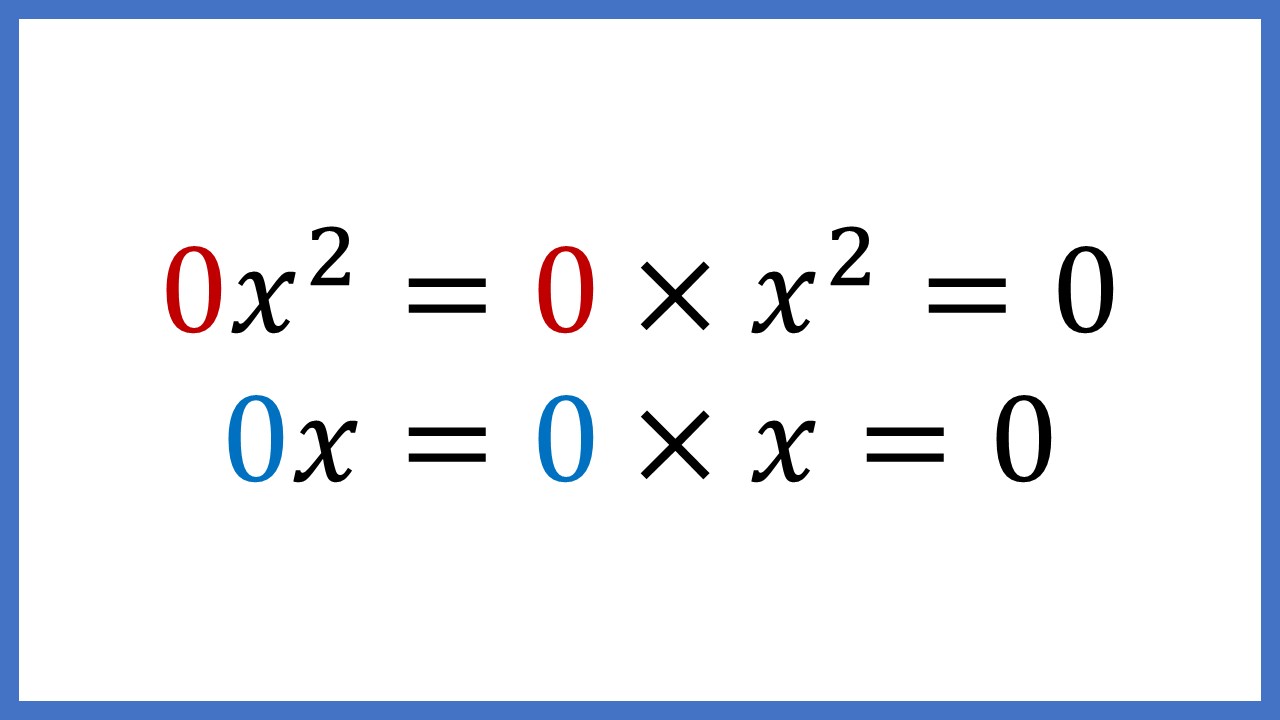
そして、解の公式は次のとおりです。わかりやすいように色分けしています。
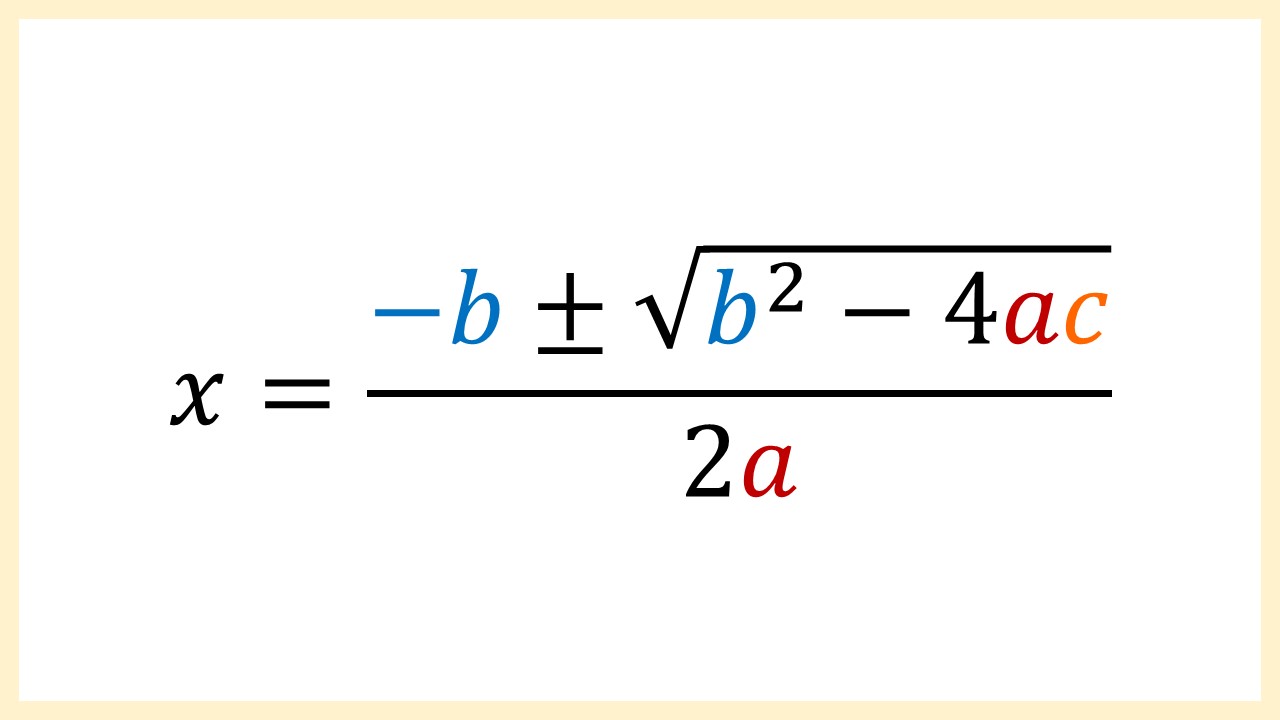
この式には±(プラスマイナス)があります。これの意味ですが、2次方程式の解(xの値)は2つあるので、「+の場合」と「-の場合」に分けて計算しましょう……ということです。
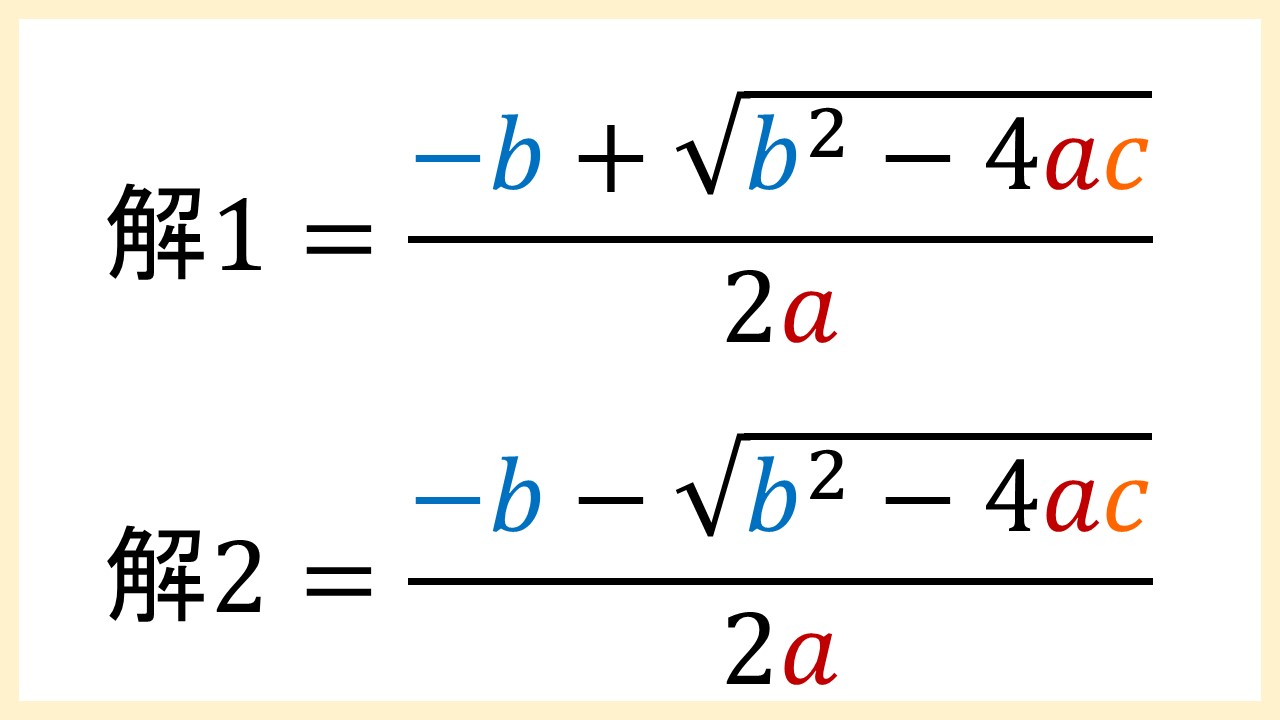
ただ、上の画像のように式を書くと、文字数が多くなってごちゃごちゃしてしまいます。
したがって、ここでは解の公式を次のように表します。
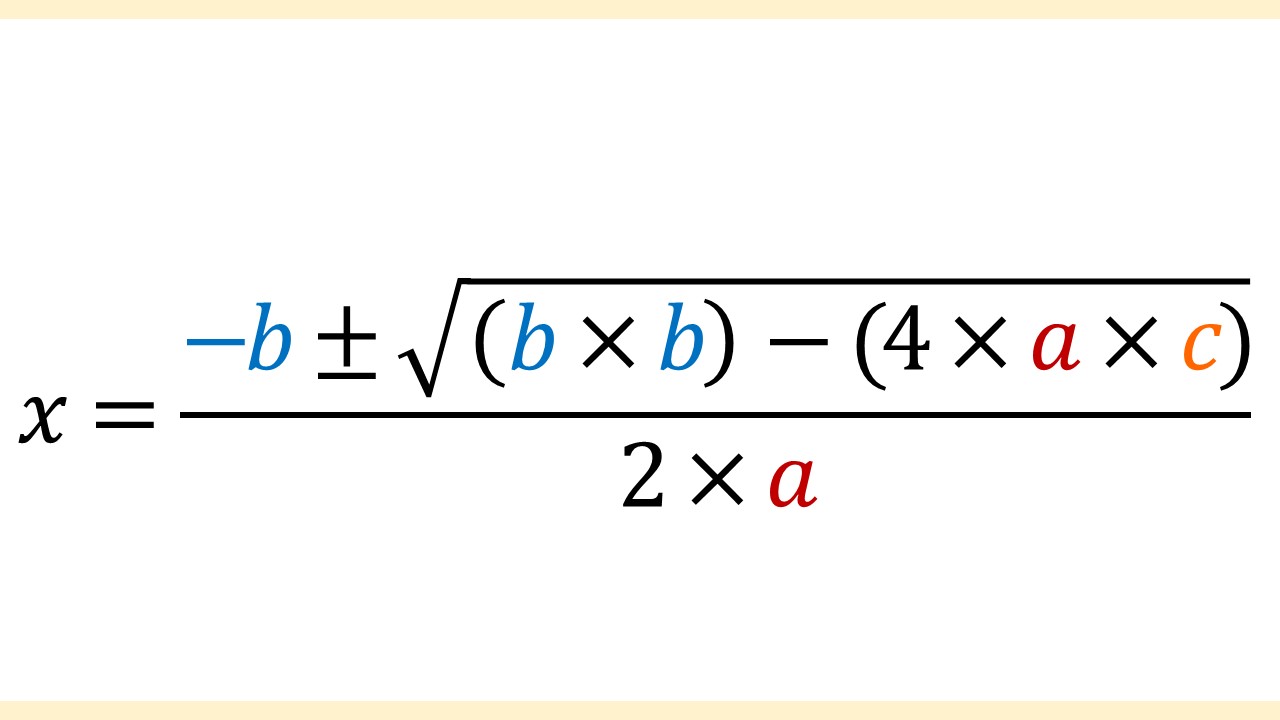
この式なら、数学が苦手な人でも理解しやすいのではないでしょうか?
まあ、√(ルート)が出てくるのは仕方がないので、それは我慢してもらう必要がありますが……。
さて、これまでのことを1枚の画像でまとめると、次のようになります。
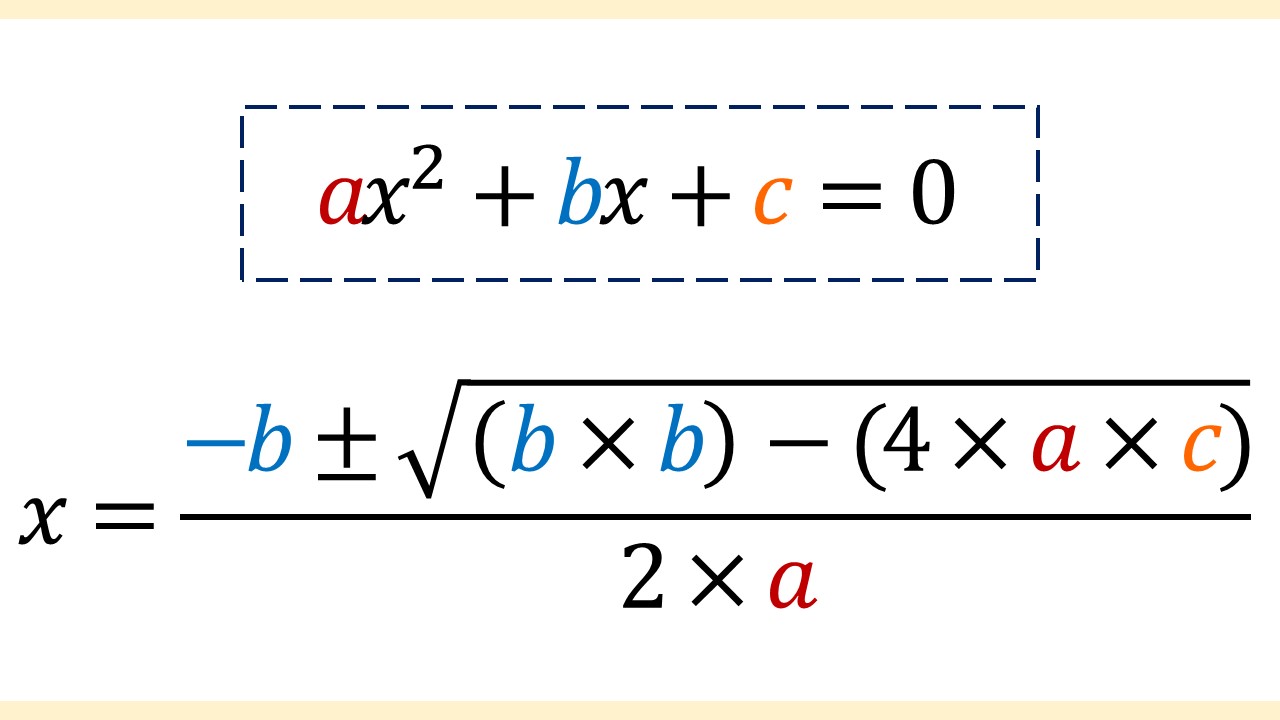
点線で囲まれたような形式の(右辺が0の)2次方程式になら、下の解の公式が使えることを意味しています。
上の画像は超重要なので、どこかにメモしておくことをおすすめします!

この解の公式を暗記して使えるようにすることで、2次方程式を確実に解くことができます!
解の公式を使った例題
それでは、例題を一緒に解いていきましょう。

2次方程式の右辺が0になっているので、解の公式が使えます! それでは、この2次方程式の係数を解の公式に当てはめていきます。
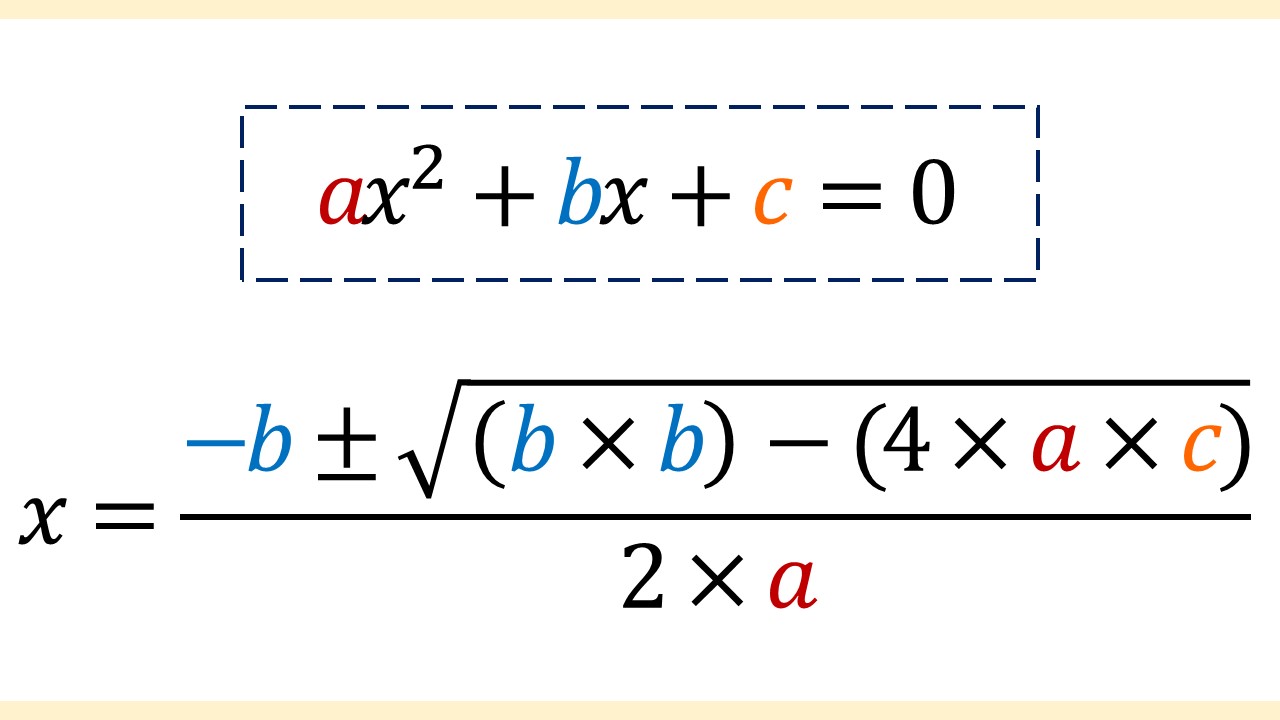
↓
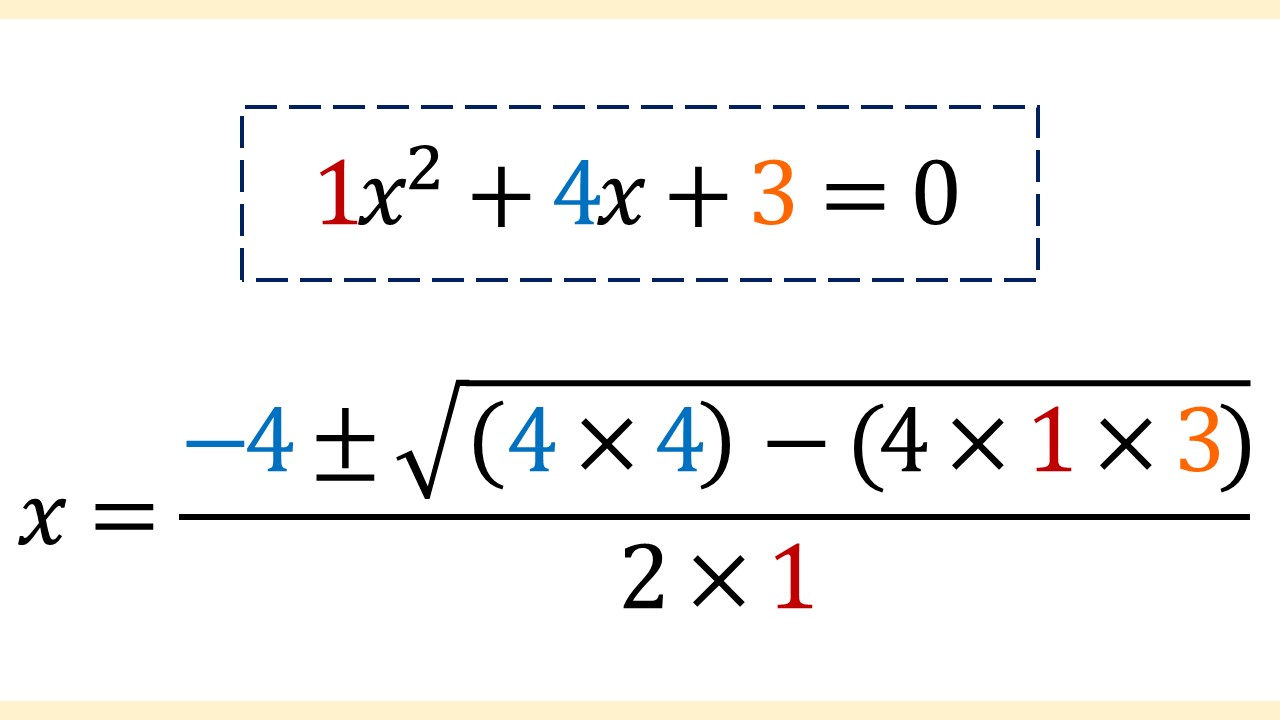
※xの2乗の係数やxの係数が書かれていないのは「1」です。なぜなら、係数の1は一般的に省略されるからです。
解の公式に当てはめることができたので、あとは計算していきます。
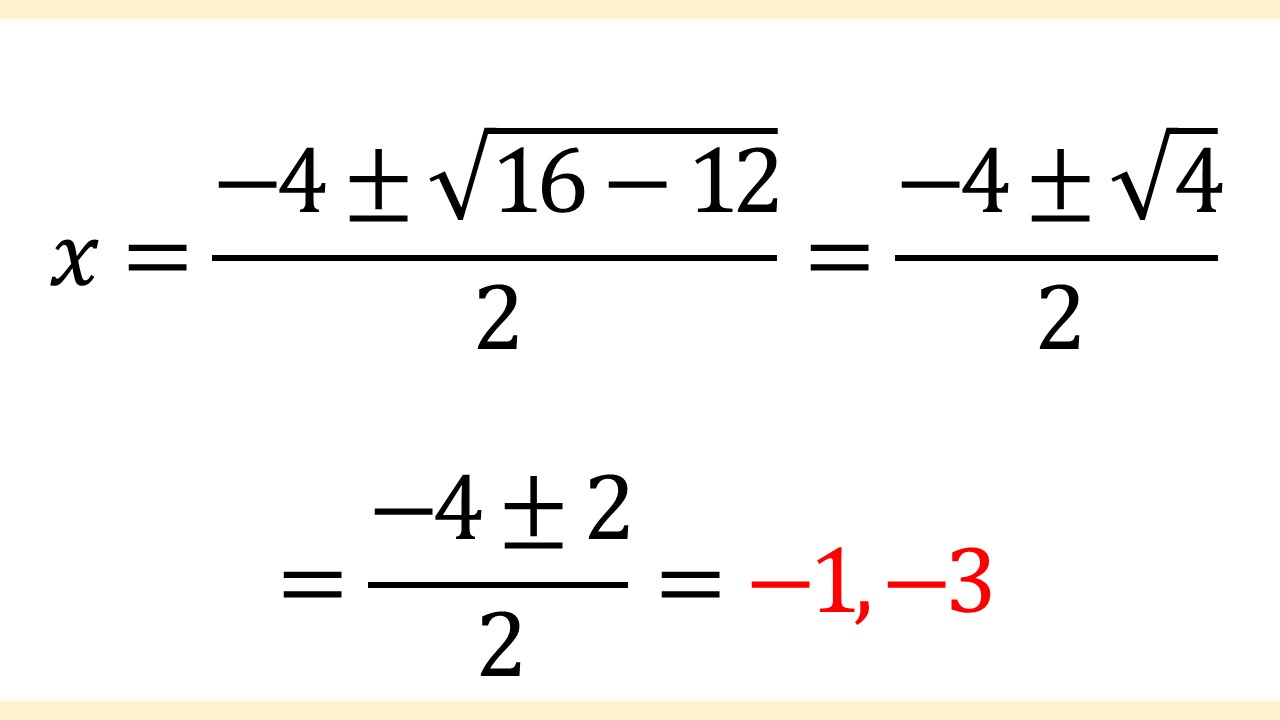
よって、解(xの値)は-1と-3であることがわかりました! 答えの書き方としては、x = -1, -3という形式が一般的だと思います。
ちなみに、プラスの場合とマイナスの場合に分けた後の途中式は、次のとおりです。場合分け後の計算がわからない人は確認してください。

では、次の例題にいきます。

2次方程式の右辺が0になっているので、解の公式が使えます! それでは、この2次方程式の係数を解の公式に当てはめていきます。
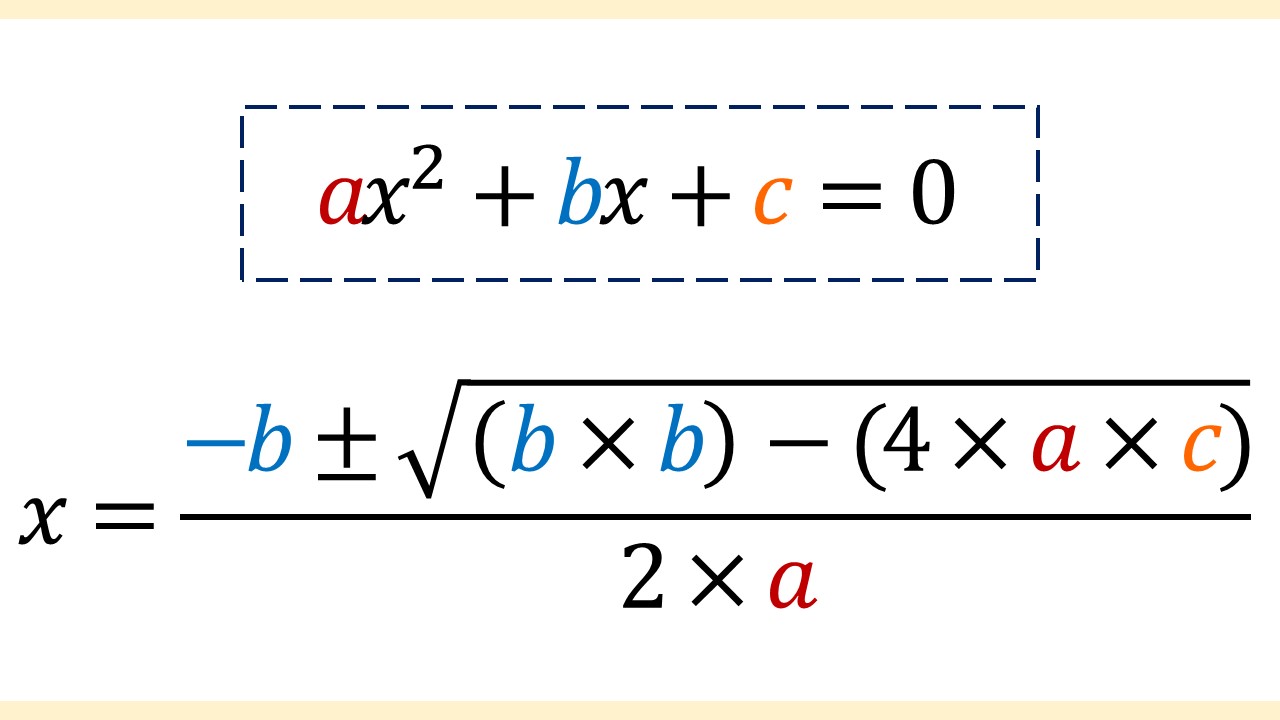
↓
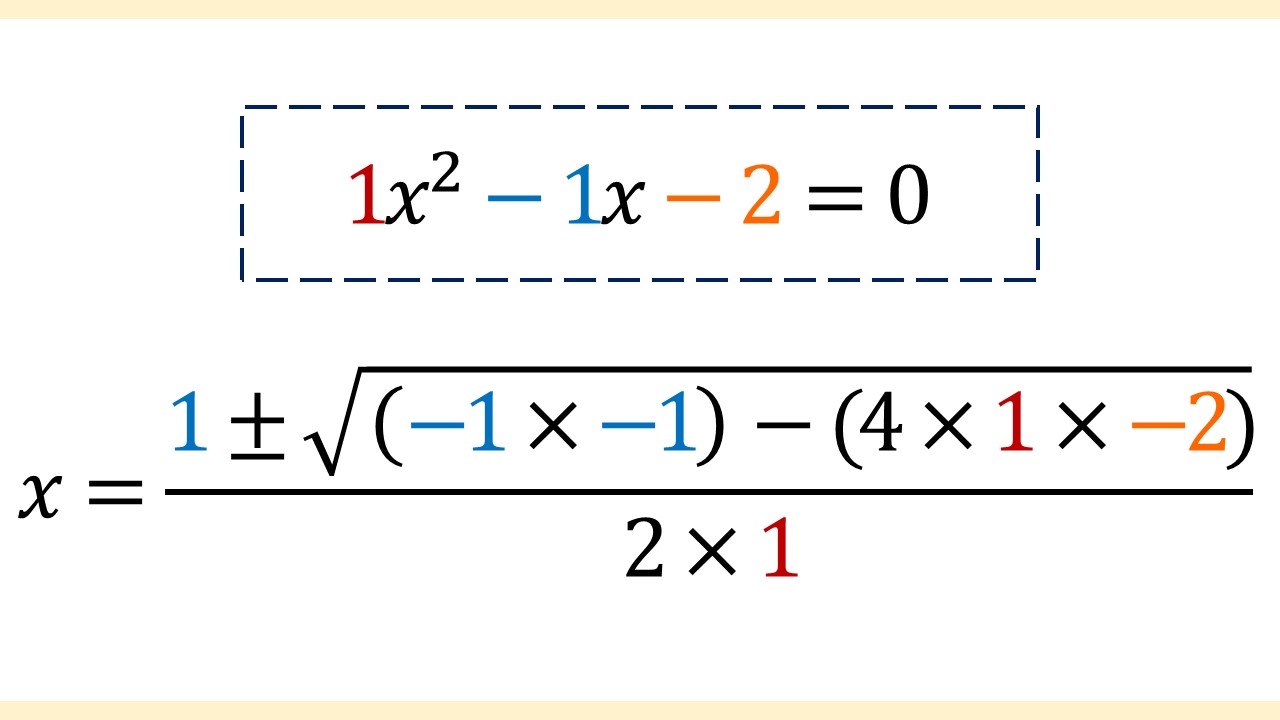
※xの2乗の係数やxの係数が書かれていないのは「1」です。なぜなら、係数の1は一般的に省略されるからです。
-bにマイナスの値を当てはめたとき、符号はプラスになることに注意してください。例えば、-bに-1を当てはめたら1になります。
解の公式に当てはめることができたので、あとは計算していきます。
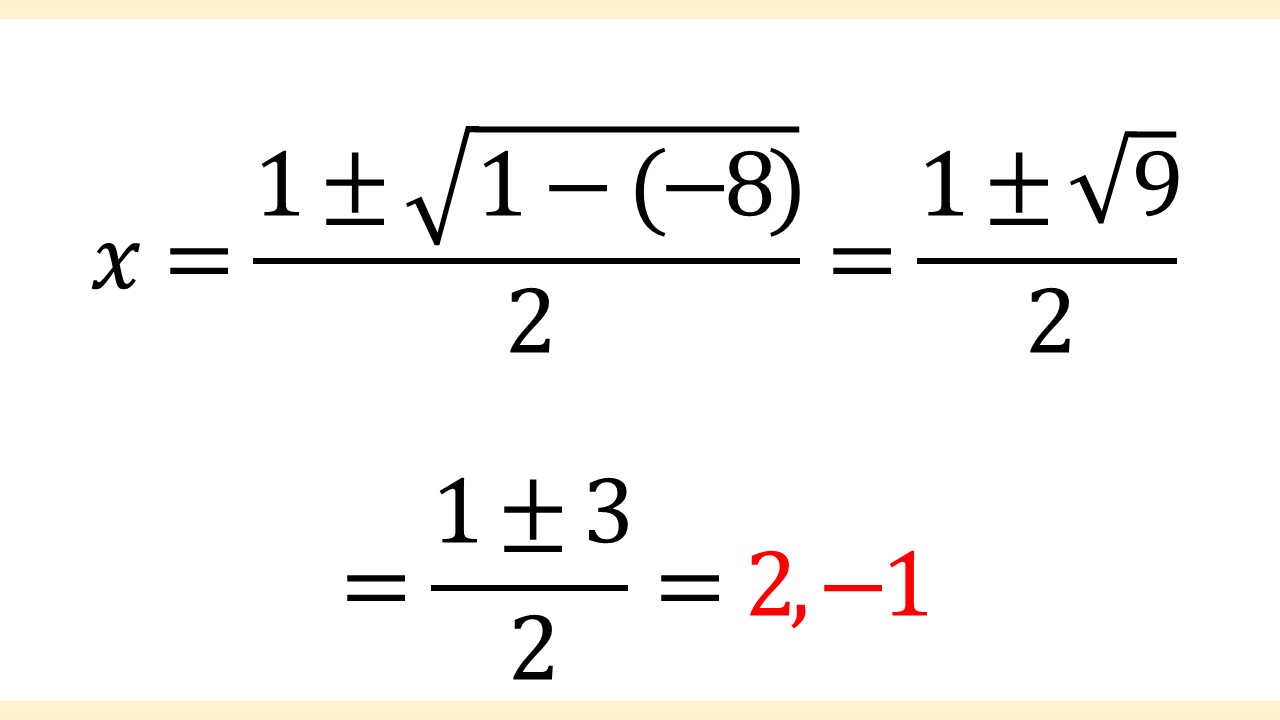
よって、x = 2, -1だとわかりました!
ちなみに、場合分け後の途中式は次のとおりです。

では、最後の例題にいきます。

2次方程式の右辺が0になっているので、解の公式が使えます! それでは、この2次方程式の係数を解の公式に当てはめていきます。
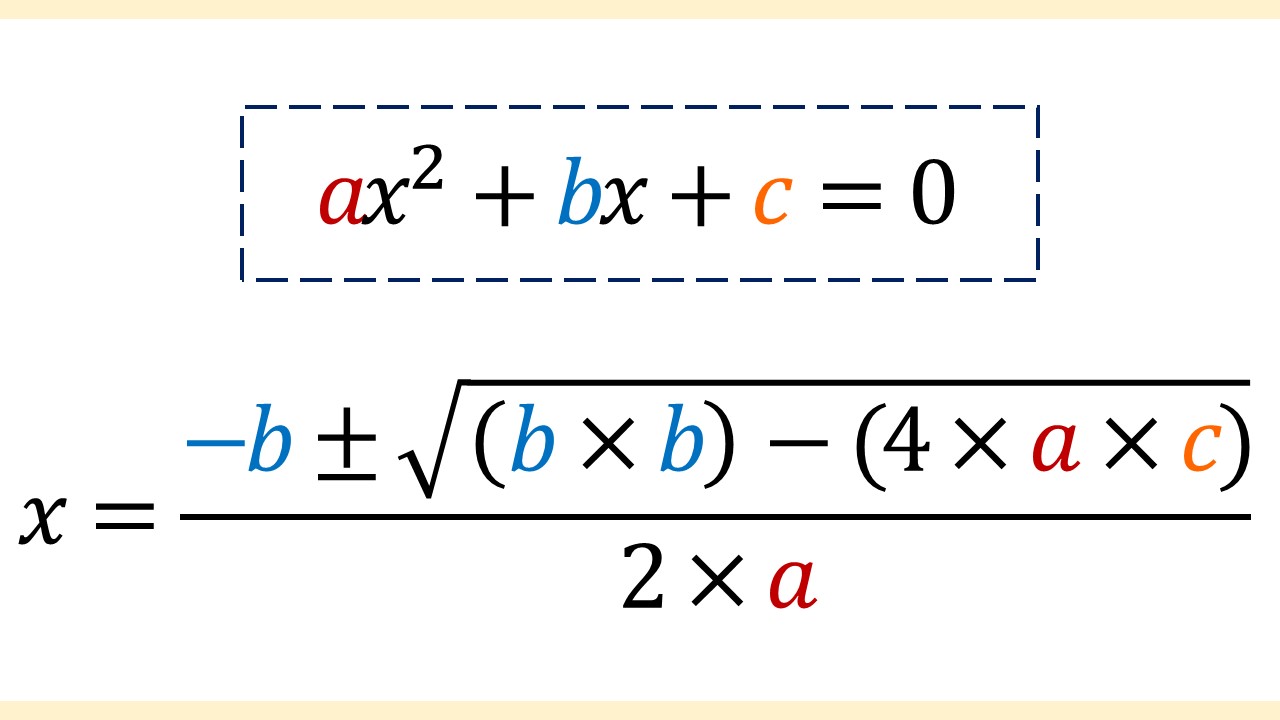
↓
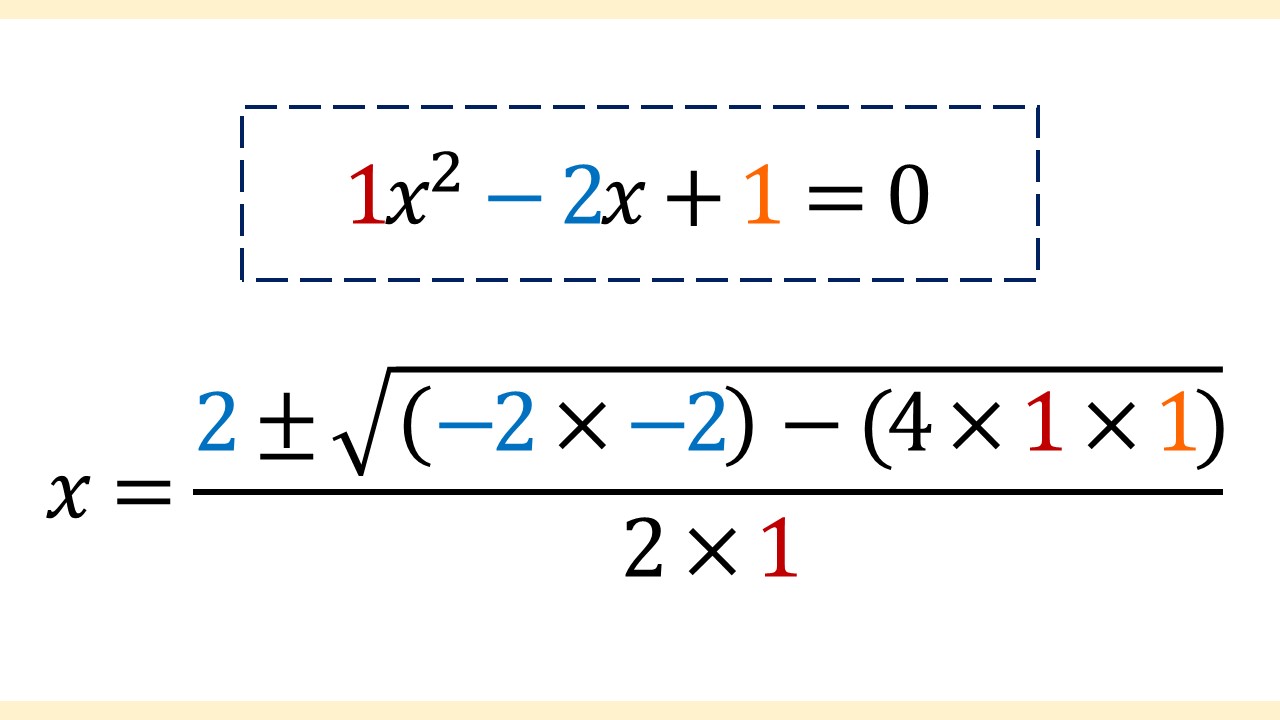
※xの2乗の係数やxの係数が書かれていないのは「1」です。なぜなら、係数の1は一般的に省略されるからです。
-bにマイナスの値を当てはめたとき、符号はプラスになることに注意してください。例えば、-bに-2を当てはめたら2になります。
解の公式に当てはめることができたので、あとは計算していきます。
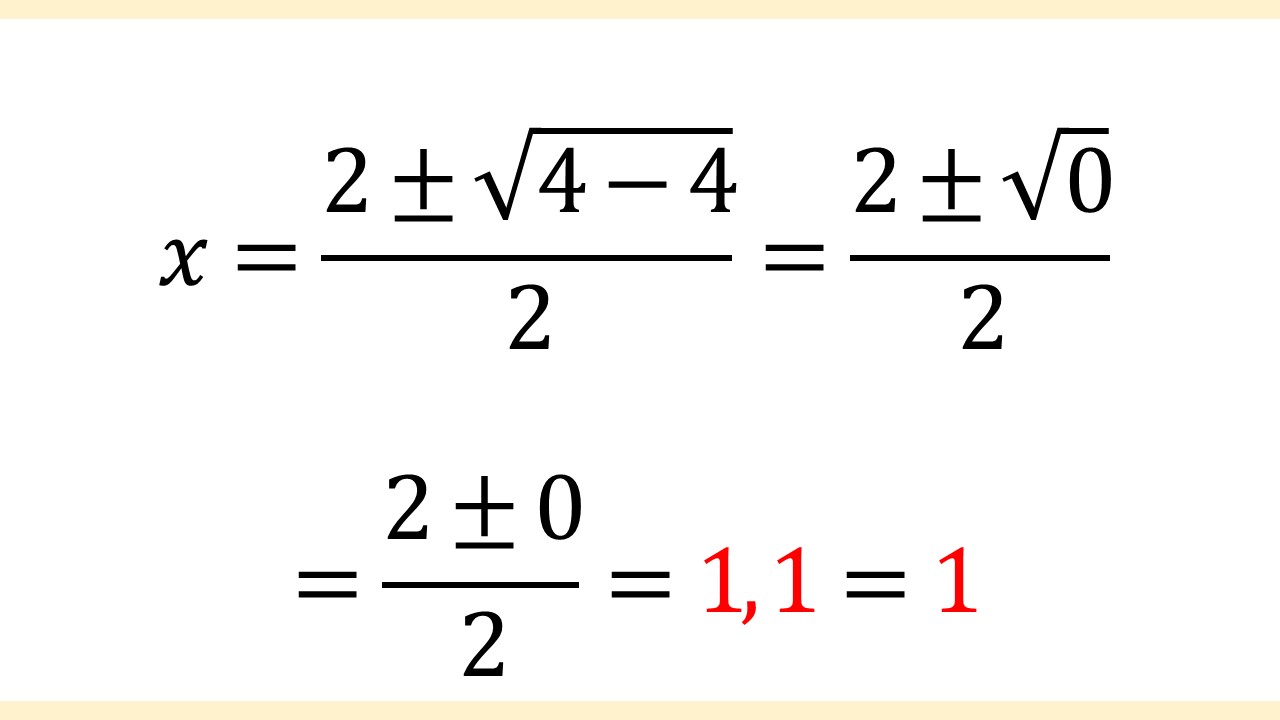
よって、x = 1, 1だとわかりました!
場合分け後の途中式は次のとおりです。示す意味がほとんどないですが……(笑)。

ここで、「あれ? xが2つとも一緒の値になっちゃったけど、これって大丈夫なの?」と思った人もいるかもしれませんが、これが正解です。
同じ値の解のことを「重解」といって、x = 1(重解)というように書きます。
このように、2次方程式の解が絶対に2つあるとは限りません。重解のように、解が1つになる場合もあります。
また、虚数解というものもあるのですが、複素数の知識が必要になりますので、ここでは考えないものとします。
……ここまでが、解の公式の基礎です。
もし不安なら、記事の最初から再チェックしてみてください。

それでは、練習問題に挑戦してみてください。問題はあまり難しくはありません。
2次方程式の確認問題集
問題編
【1】次の2次方程式を、解の公式を使って解きましょう。
(1)

(2)

(3)

(4)

(5)

※右辺の値に注意してください。
解答編
【1】次の2次方程式を、解の公式を使って解きましょう。
(1)

右辺が0なので、解の公式が使えますね。この2次方程式の係数を、解の公式に当てはめていきます。
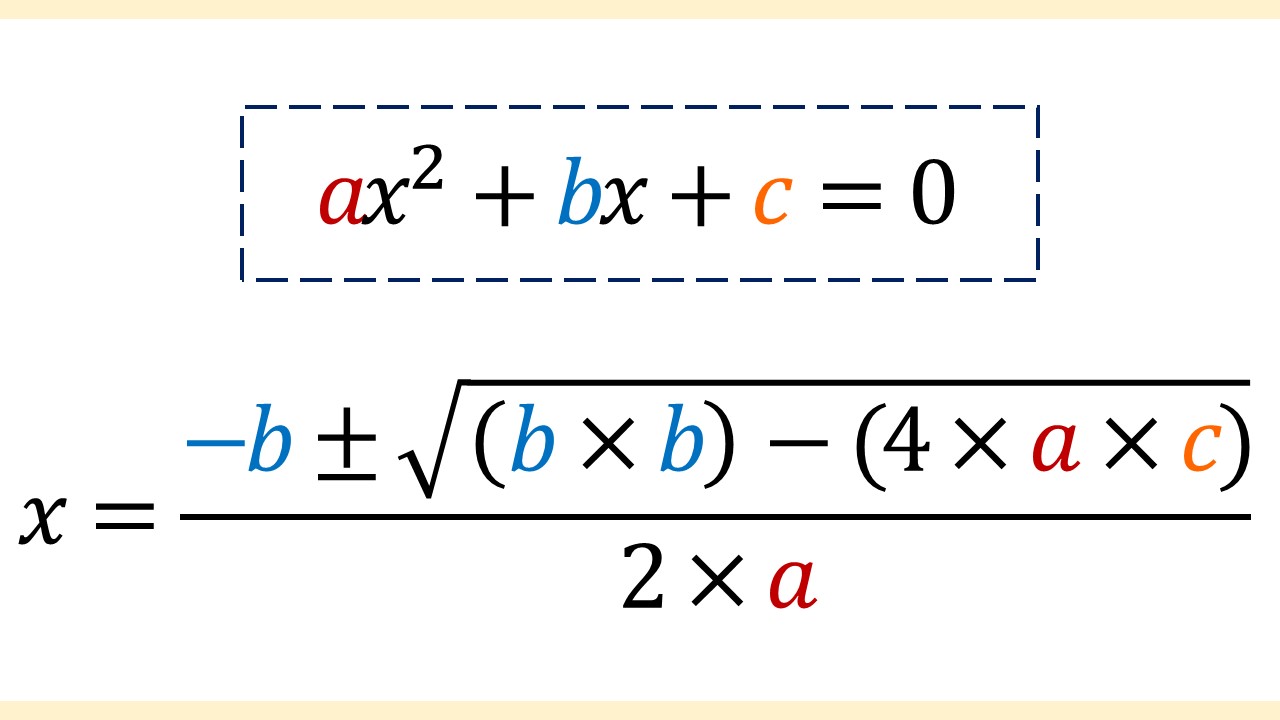
↓
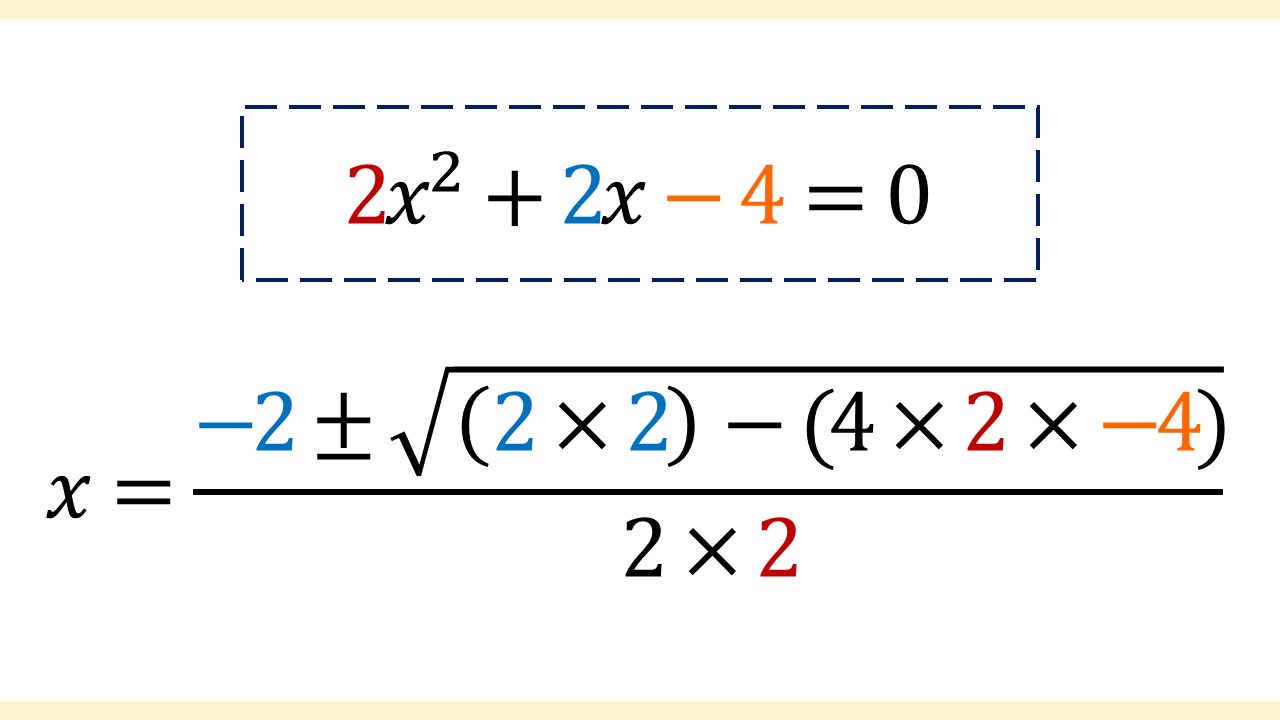
当てはめたので、あとは計算していきます。
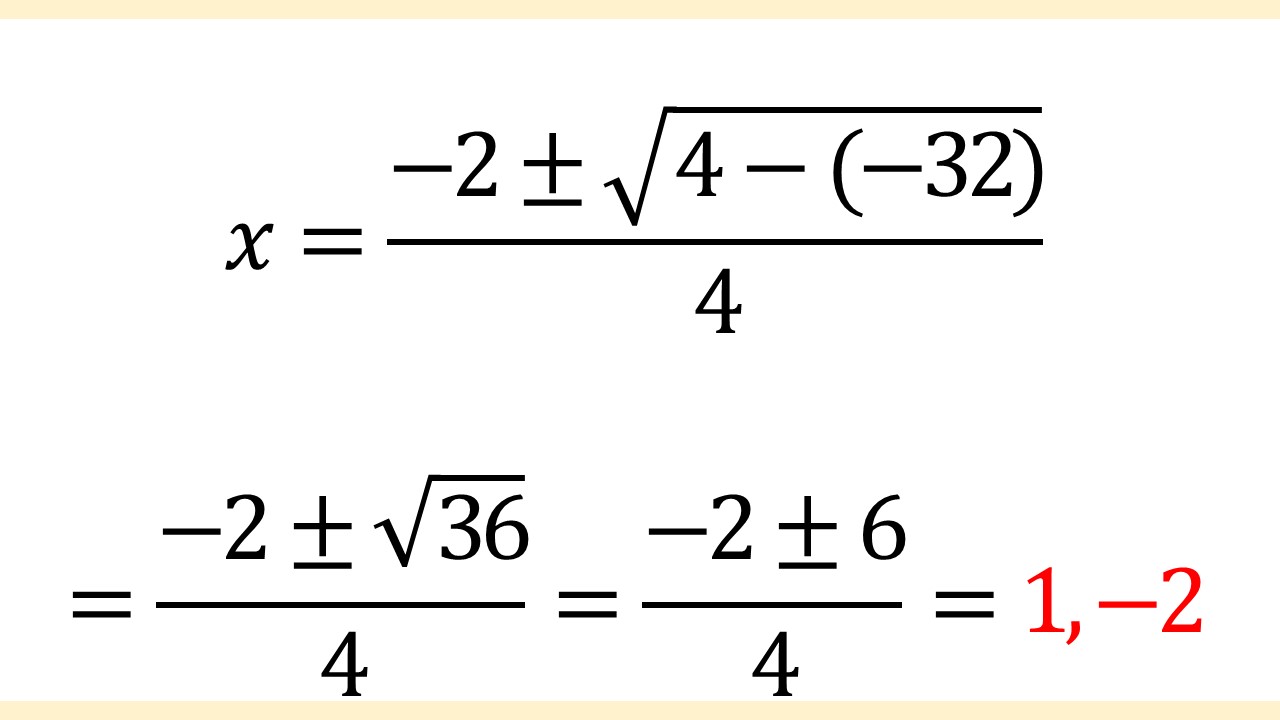
よって、答えはx = 1, -2です。
ちなみに、場合分け後の途中式は次のとおりです。

(2)

右辺が0なので、解の公式が使えますね。この2次方程式の係数を、解の公式に当てはめていきます。
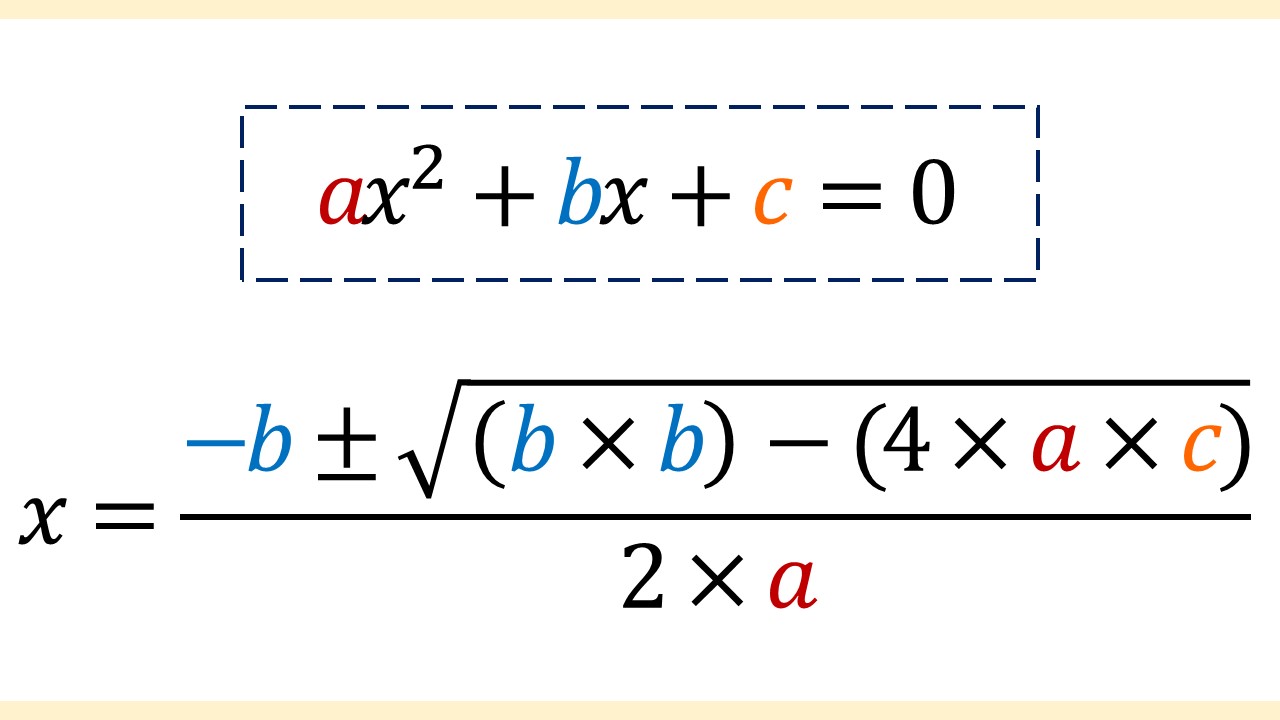
↓
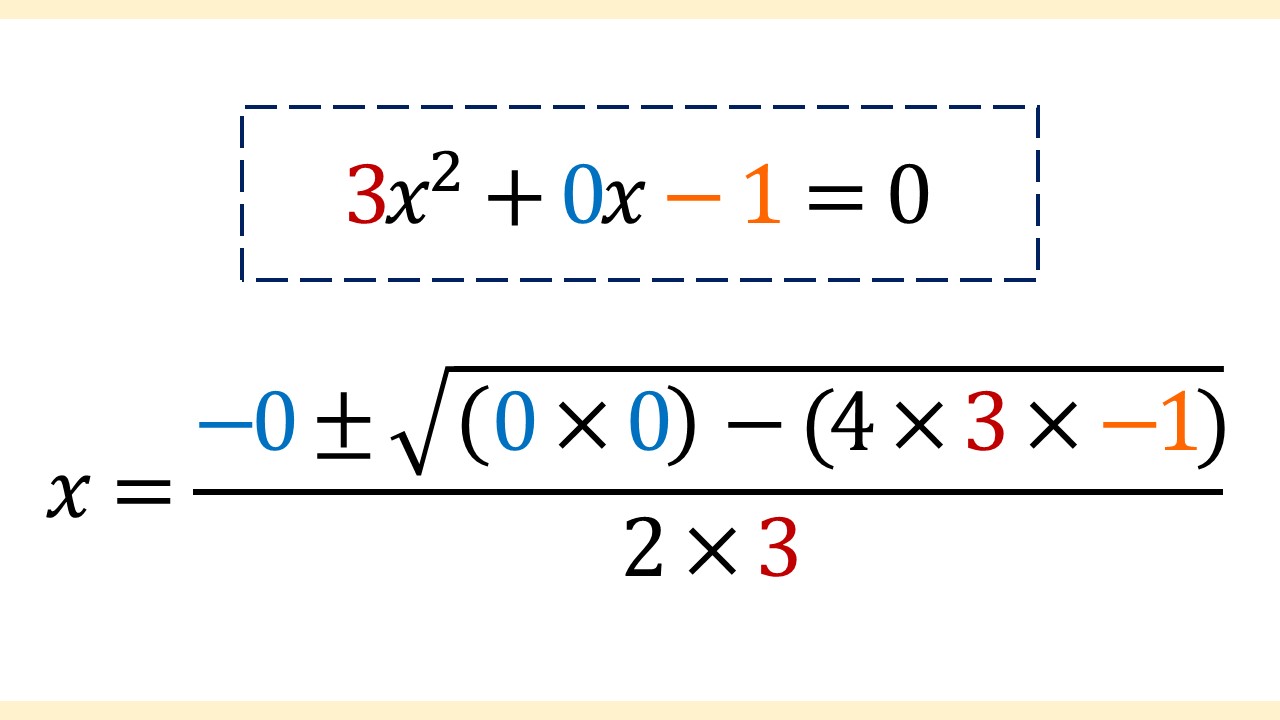
xの項が存在しないので、bの値が0であることに注意してください。
当てはめたので、あとは計算していきます。
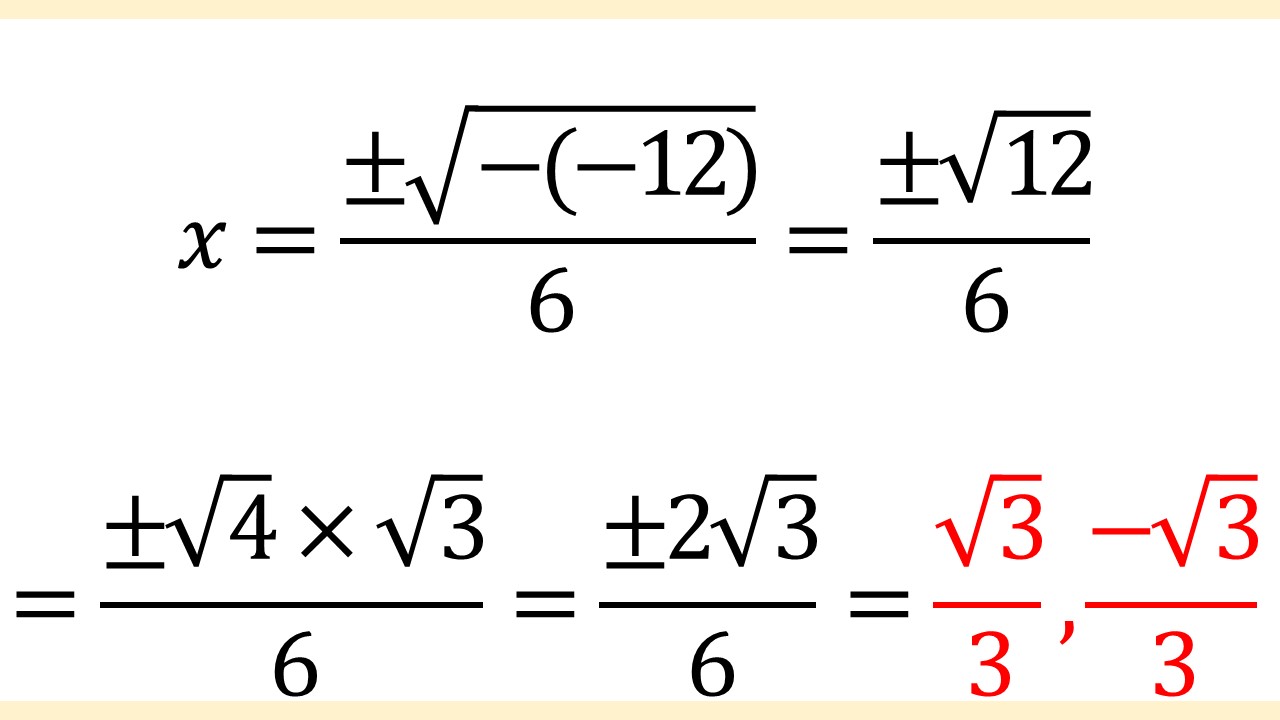
よって、答えはx = (√3)/3, (-√3)/3です。
ちなみに、場合分け後の途中式は次のとおりです。
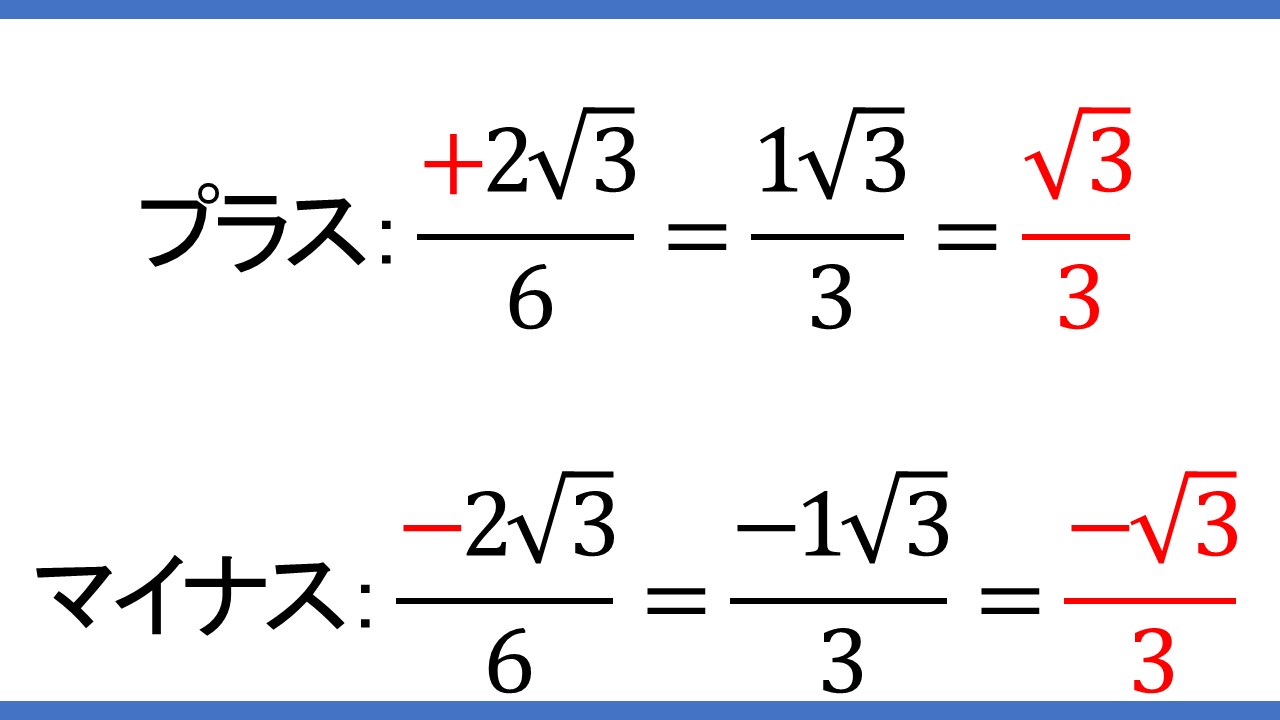
√3は整数にできないので、そのままの状態にしておきます。
(3)

右辺が0なので、解の公式が使えますね。この2次方程式の係数を、解の公式に当てはめていきます。
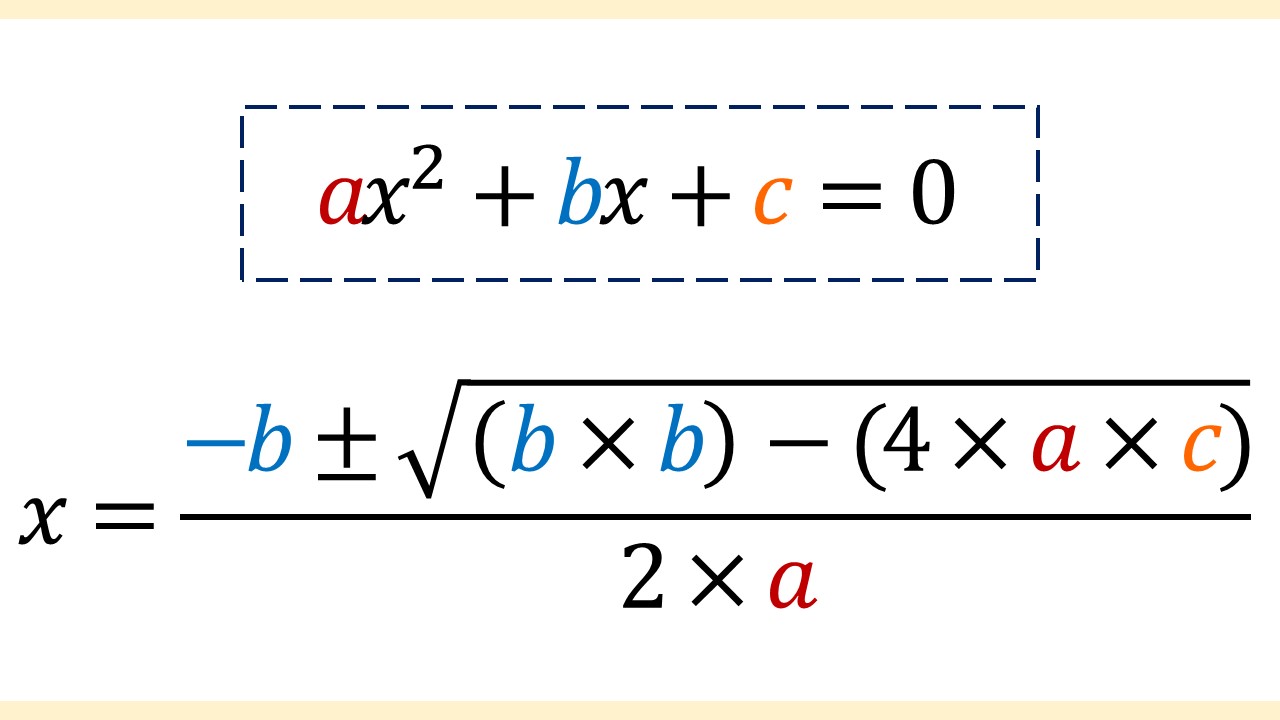
↓
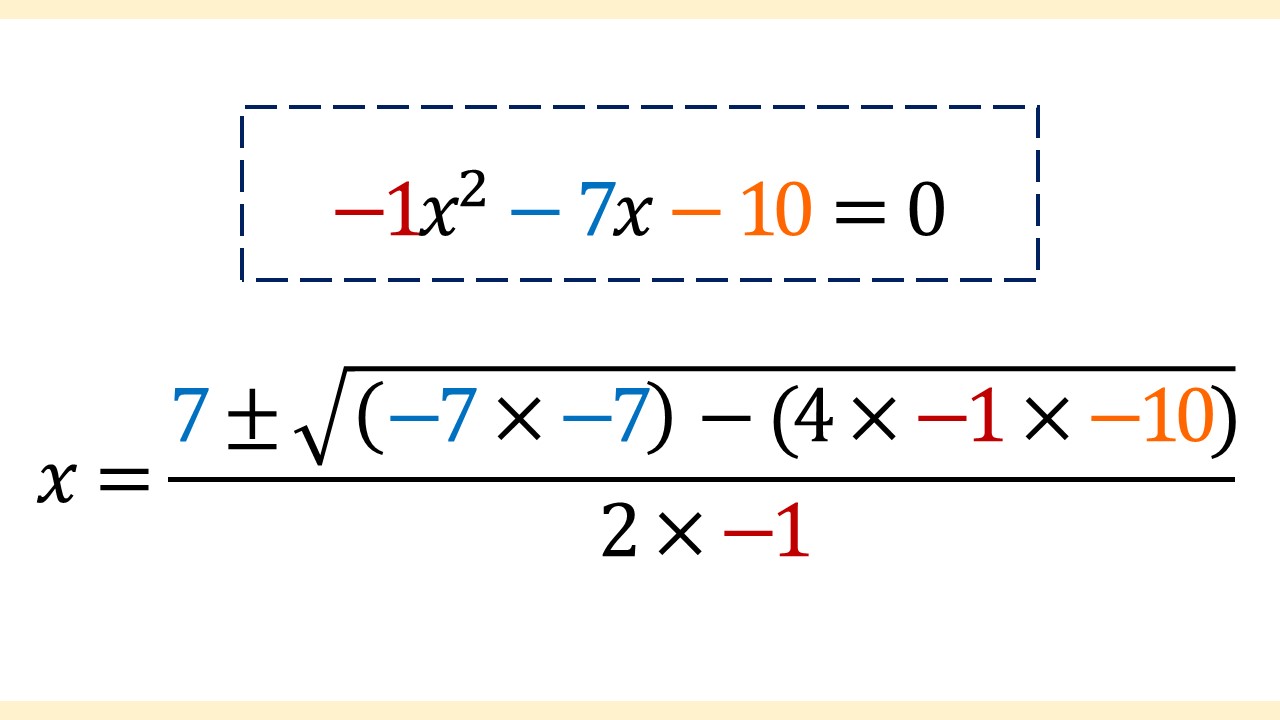
当てはめたので、あとは計算していきます。
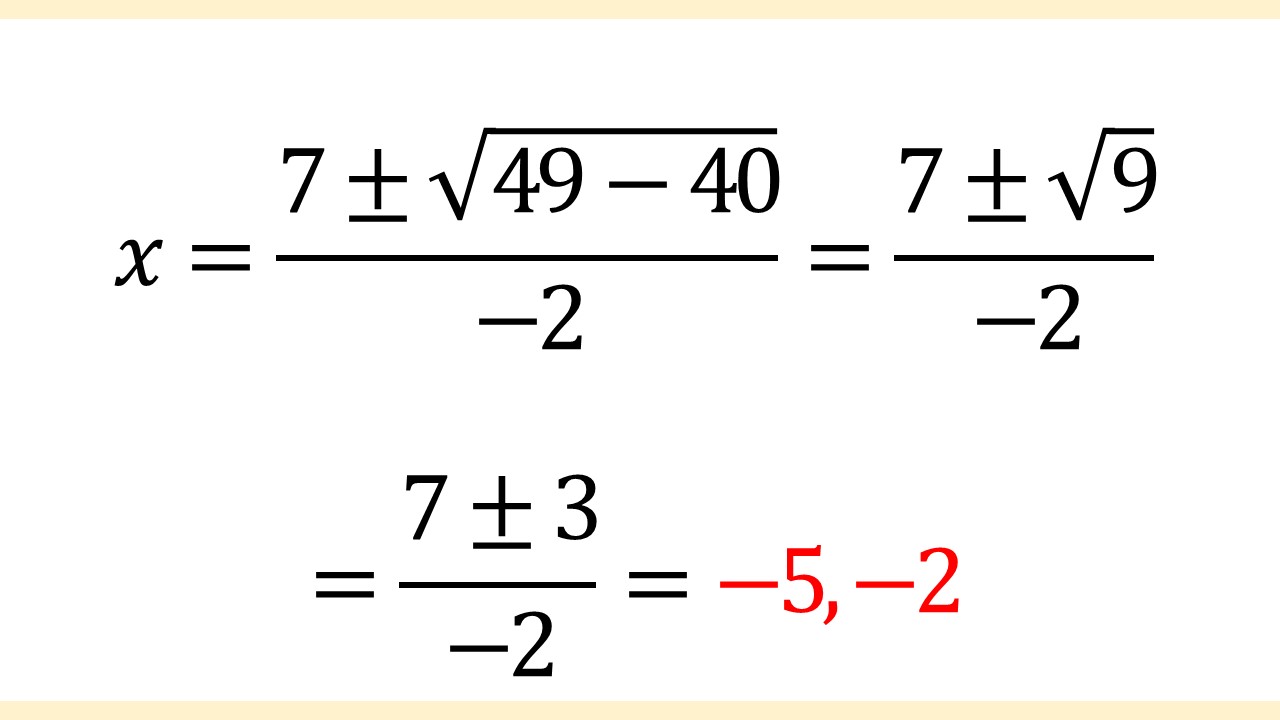
よって、答えはx = -5, -2です。
ちなみに、場合分け後の途中式は次のとおりです。

(4)

右辺が0なので、解の公式が使えますね。この2次方程式の係数を、解の公式に当てはめていきます。
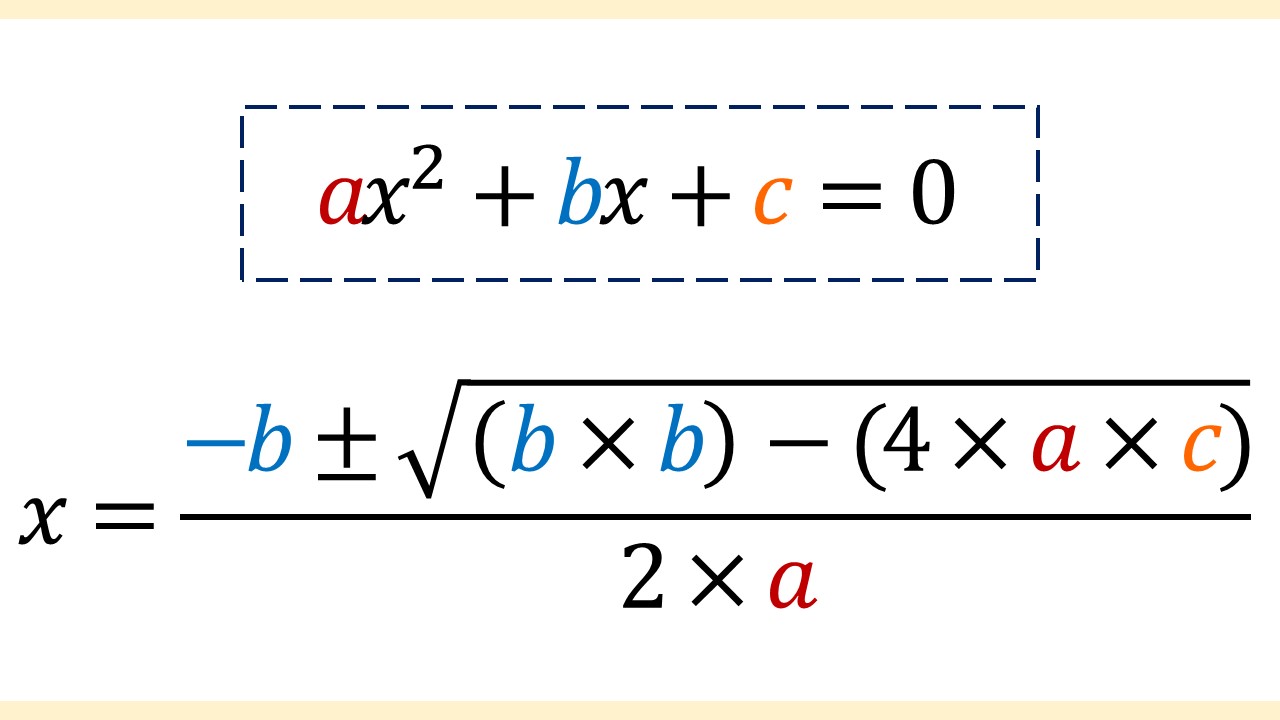
↓
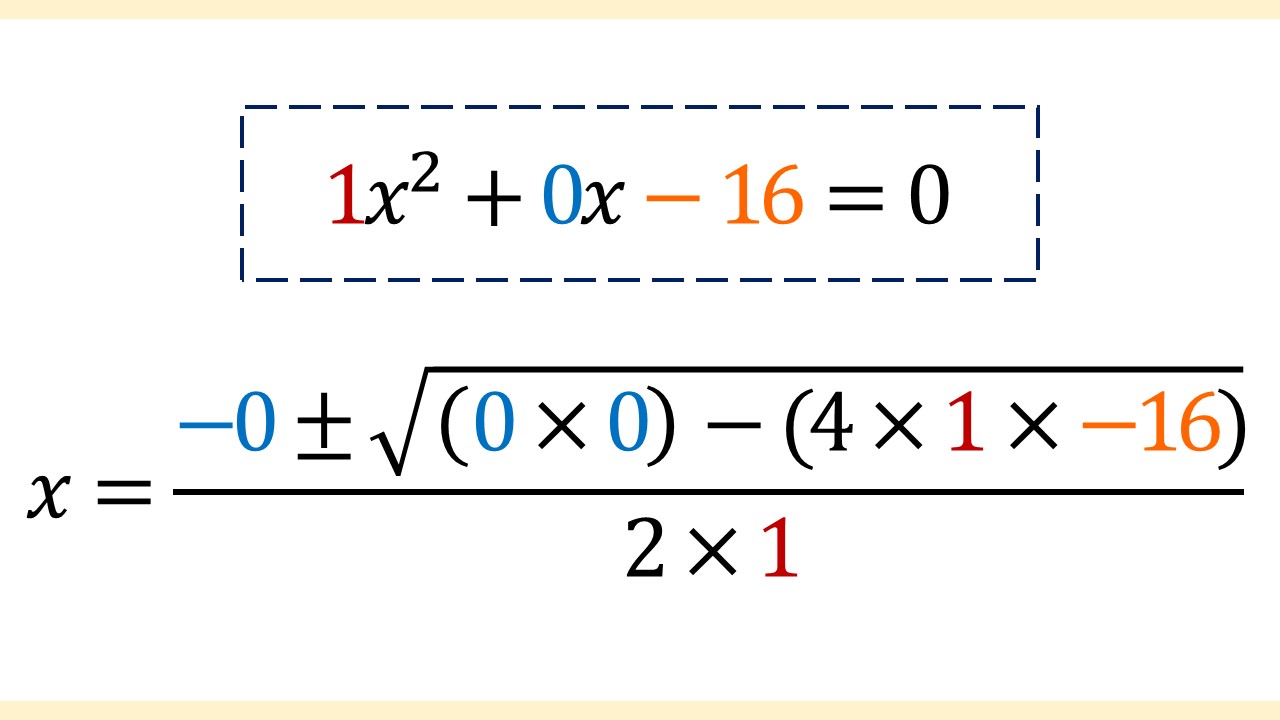
xの項が存在しないので、bの値が0であることに注意してください。
当てはめたので、あとは計算していきます。
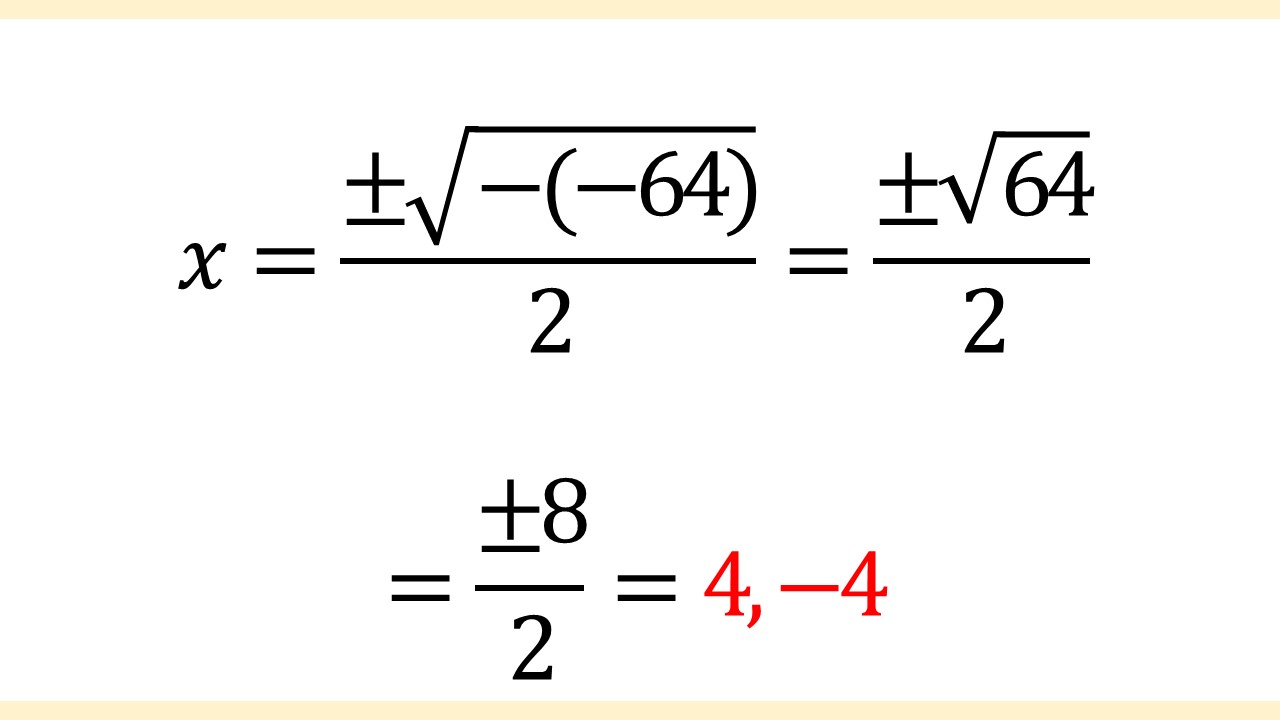
よって、答えはx = 4, -4です。
ちなみに、場合分け後の途中式は次のとおりです。

(5)

右辺が0ではないので、このままでは解の公式が使えません。したがって、解の公式を使えるように式を少し変形します。

移項することで、解の公式が使えるようになりました! それでは、この2次方程式の係数を、解の公式に当てはめていきます。
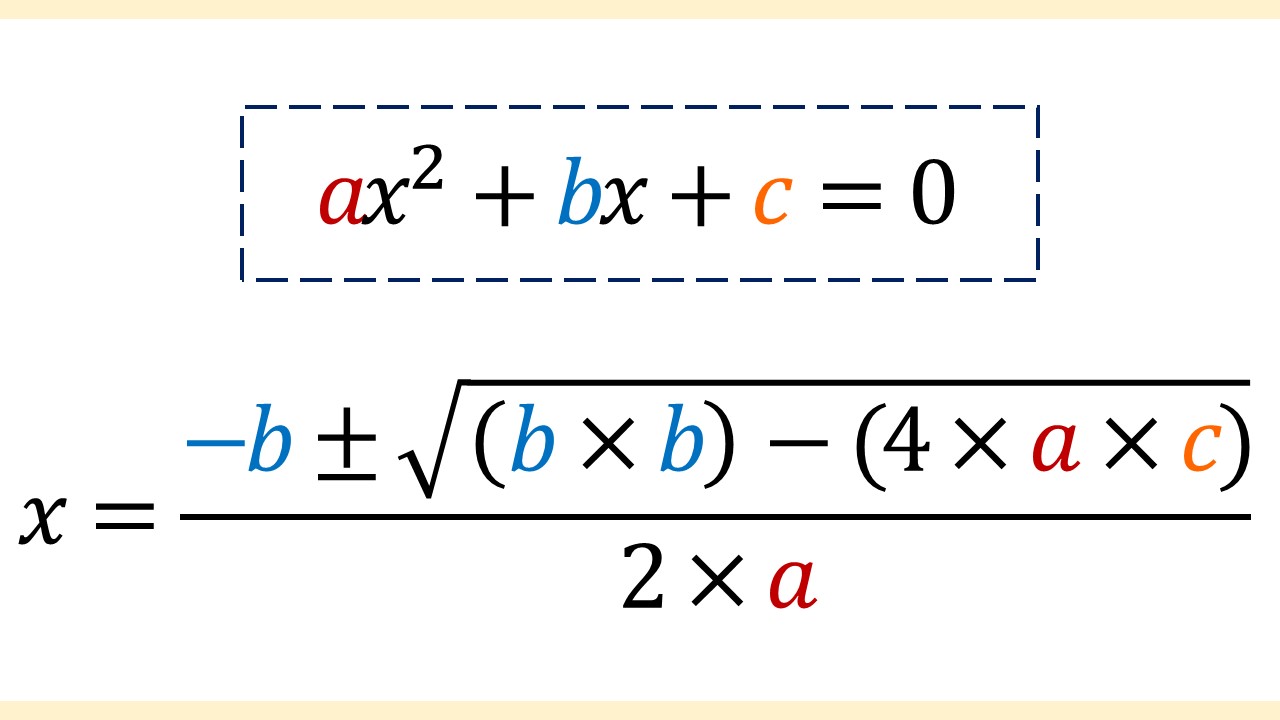
↓
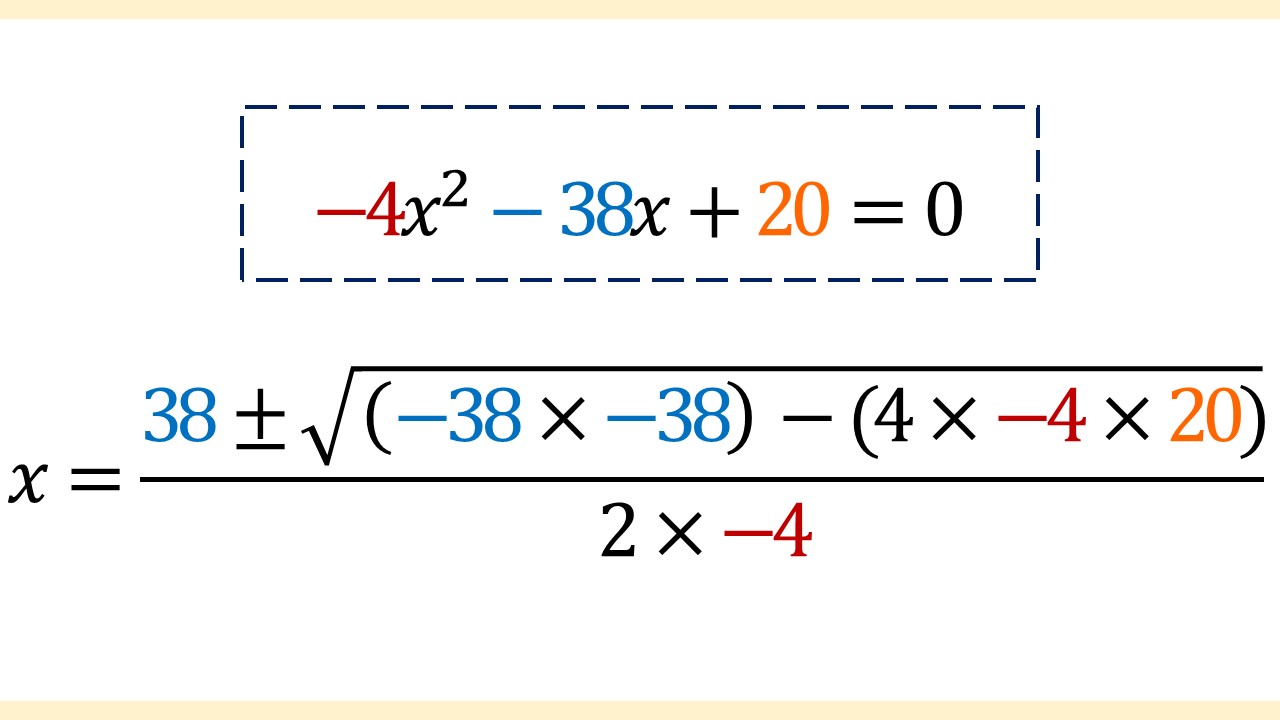
当てはめることができたので、あとは計算していきます。値が大きいので、計算が面倒です。
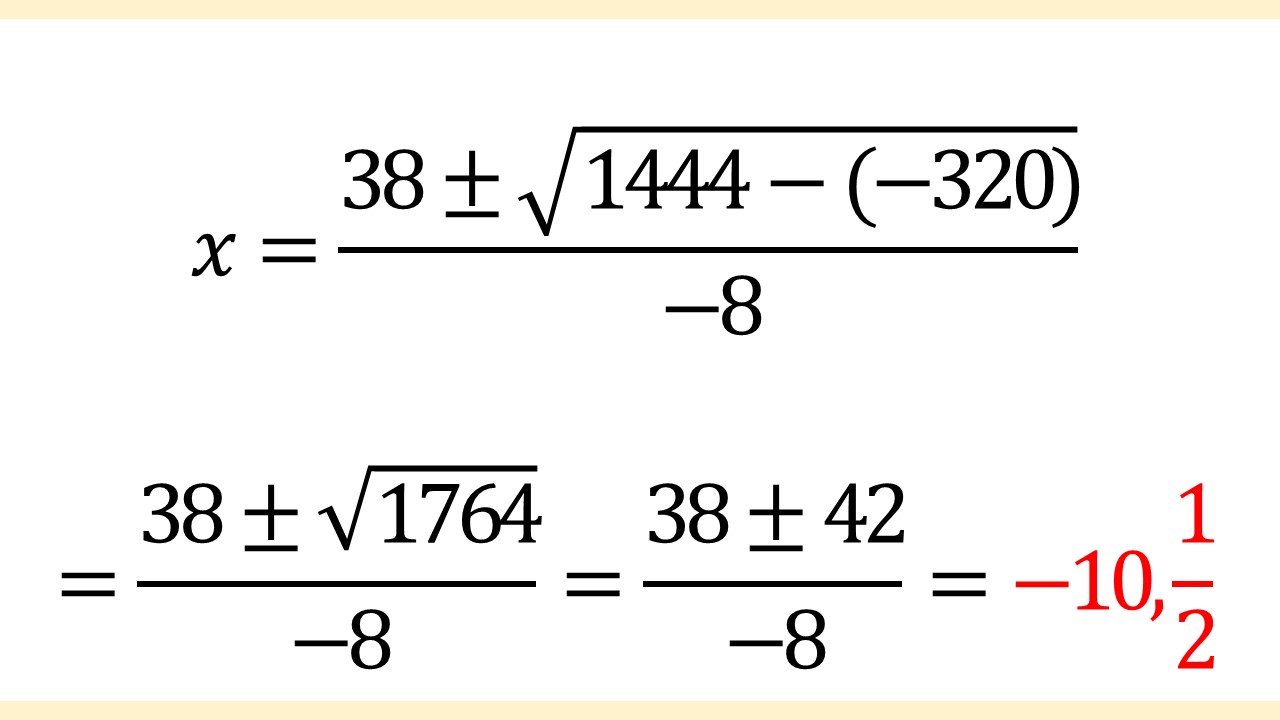
よって、答えはx = -10, 1/2です。
√1764(2乗したら1764になる値)を整数にするコツですが、例えば、50の2乗は2500になるので、50の2乗よりは小さいことがわかりますよね。 次に、40の2乗は1600になるので、40の2乗よりは大きいことがわかります。
つまり、40と50の間にある整数を、それぞれ2乗にして1764にならないかをチェックしていけばOKです。そうすれば、42であることがわかります。手間はかかりますが、確実な方法です。
ちなみに、場合分け後の途中式は次のとおりです。
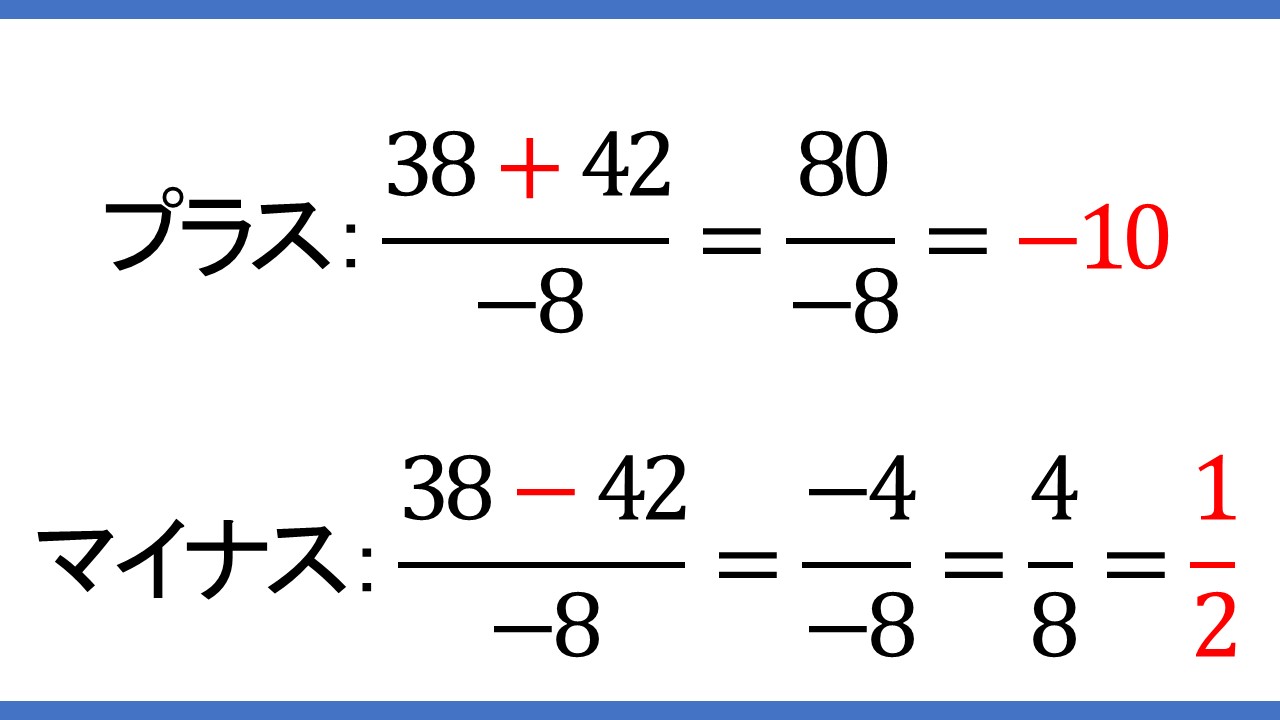
ここまでの内容を理解できたのなら、解の公式の基礎はバッチリです! これで、答えが実数解となる2次方程式は解けるはずです。

説明がかなり長くなってしまいました。本当にお疲れさまでした。




